Les mathématiques employées par le physicien sont tournées autour de la résolution d'équations différentielles, du calcul d'intégrales, de l'algèbre linéaire... Chaque fois que cela est possible on recherche une solution analytique, c'est à dire une ou plusieurs expressions mathématiques où un ensemble de variables et de constantes expriment la solution du problème recherché. L'intérêt d'une telle démarche est évident. On peut rapidement comprendre les relations entre les différents paramètres, porteurs d'une signification physique. L'analyse du phénomène et de son évolution, en fonction des conditions de l'expérience est simplifiée.
Les cours de physique classique sont friands d'une telle démarche car elle est très pédagogique: elle permet d'appréhender simplement tous les aspects de la théorie étudiée. Malheureusement cette approche est aussi réductrice car il est très souvent nécessaire de simplifier les équations pour trouver une solution. Le physicien introduit les approximations indispensables à la résolution analytique des équations. Ces simplifications doivent être justifiées et réduisent la généralité de la théorie qui soustend le phénomène physique étudié. Le physicien recherche les approximations qui lui permettront à la fois de résoudre ses équations et de maintenir la plus grande généralité quand aux conclusions qui en résulteront.
En voici un exemple très simple.
Dans la théorie de l'attraction universelle établie par
Newton deux masses M et m, que nous supposerons ponctuelles s'attirent mutuellement.
Elles sont soumises à une force: ![]()
où G représente la constante d'attraction universelle
et r la distance entre les deux masses. On peut établir les équations différentielles
de leur mouvement relatif par rapport à un référentiel supposé au repos: ![]() pour la masse m,
pour la masse m,
![]() pour la masse M.
pour la masse M. ![]() est un vecteur unitaire sur la droite liant les deux masses et orienté de M
vers m (fig. 1). r12 est la distance entre les masses.
est un vecteur unitaire sur la droite liant les deux masses et orienté de M
vers m (fig. 1). r12 est la distance entre les masses. 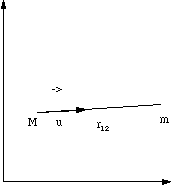
Figure 1: Deux masses en attraction mutuelle
Suivant les conditions initiales du mouvement des deux masses les solutions varient. Ce problème a été étudié dès la première année d'études de la physique à l'université.
Comment se transforme-t-il si on introduit une troisième masse?
Ecrire les équations différentielles du mouvement est à peine plus compliqué: on introduit les forces d'attraction des trois masses deux à deux et on établit trois équations différentielles pour chacune des masses en indiquant dans le deuxième membre la somme des deux forces auxquelles chacune de ces masses est soumise:
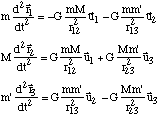
Les notations se déduisent des précédentes.
Le problème, en apparence, n'est guère plus compliqué mais il apparaît maintenant une difficulté de taille: il n'existe aucune méthode analytique pour résoudre ce système de trois équations différentielles liées. Le physicien se trouve donc devant deux choix:
| simplifier le problème pour se ramener au cas précédent. Cela signifie qu'on négliger l'influence de la troisième masse m'. Ceci doit être justifié et vérifié. On introduit une hypothèse simplificatrice donc réductrice pour résoudre ce problème. | |
| remplacer ce calcul analytique par un calcul numérique effectué au moyen d'un ordinateur si les simplifications envisagées sont trop grossières. Les seules approximations sont alors celles de la méthode numérique choisie pour intégrer les équations et les limitations introduites par l'ordinateur qui sert à les calculer. Nous reviendrons plus tard sur ces aspects très important des méthodes numériques. |
Recourir à un calcul numérique nécessite des moyens supplémentaires par rapport à la feuille de papier. Le principe même de la technique employée ne permet pas d'établir une solution générale du problème qui permette de l'appréhender dans sa globalité. La loi recherchée est donc difficile à exprimer puisqu'elle ne peut s'écrire sous la forme d'une formule mathématique. Chaque ensemble de conditions initiales (positions et vitesses des masses) exige un nouveau calcul. Il faut donc construire un programme que l'on emploiera de nombreuses fois en faisant varier les données du problème, c'est à dire, dans le cas présent, les conditions initiales: vitesse et position des masses. Ceci est le plus grand défaut de la méthode: il n'est plus possible de prévoir des évolutions possibles d'un phénomène (forme et changement des dimensions des orbites des masses) par la simple analyse des équations. L'analyse du mouvement ne pourra se faire qu'en traçant des ensembles d'orbites pour différentes conditions initiales et en rapprochant l'ensemble de ces résultats. En fait on effectue une expérience numérique de physique. Le programme est un moyen pour simuler l'expérience.
L'histoire de l'étude numérique de l'interaction à N corps est intéressante. Les physiciens qui programmaient cette étude se sont aperçus que le calcul était très sensible aux conditions initiales: un léger changement pouvait introduire de grandes différences dans les trajectoires des masses. Mieux encore il suffisait de changer la précision de quelques résultats intermédiaires pour modifier complètement l'allure du mouvement. L'étude de ces anomalies a conduit à la découverte d'un aspect complètement nouveau de la physique: la théorie du chaos. Dans certaines conditions, et compte-tenu de l'imprécision inhérente à la connaissance exacte des vitesses et positions des objets, il devient totalement impossible de prévoir les trajectoires des masses. La théorie du chaos qui a semblé, au début, échapper à la nature jusque là déterministe de la physique, n'aurait jamais était découverte sans le calcul numérique et les ordinateurs.
Envisageons maintenant un deuxième exemple: l'étude de la diffraction
de la lumière à l'infini (ou au foyer d'une lentille, ce qui revient au même)
par un trou circulaire. L'amplitude de l'onde S(X,Y) au point de coordonnées
R(X,Y) dans l'écran d'observation se déduit de l'amplitude de la lumière en
tout point de la surface du trou s(x,y) par la transformée de Fourier: ![]()
![]() représente
les coordonnées d'un point dans l'écran d'observation,
représente
les coordonnées d'un point dans l'écran d'observation, ![]() d'un point dans la source (le trou circulaire). La solution de cette intégrale
n'est analytique qu'en apparence. On montre que:
d'un point dans la source (le trou circulaire). La solution de cette intégrale
n'est analytique qu'en apparence. On montre que: ![]() où a est le rayon du trou, d la distance de l'écran d'observation et
où a est le rayon du trou, d la distance de l'écran d'observation et ![]() la
longueur d'onde de l'onde électromagnétique. J1 est la fonction de Bessel d'ordre
1, fonction bien connue des mathématiciens qui ont calculé ses valeurs numériques
(fig. 2). La figure de diffraction est formée d'anneaux circulaires alternativement
noirs et blancs.
la
longueur d'onde de l'onde électromagnétique. J1 est la fonction de Bessel d'ordre
1, fonction bien connue des mathématiciens qui ont calculé ses valeurs numériques
(fig. 2). La figure de diffraction est formée d'anneaux circulaires alternativement
noirs et blancs. 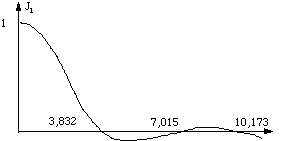 Figure
2: fonction de Bessel J1
Figure
2: fonction de Bessel J1
L'analyse de la forme de la fonction de Bessel permet de comprendre les caractéristiques principales des anneaux de diffraction. Elle ne permet cependant pas de mesurer leurs dimensions qui dépendent de la valeur de J1 qui doit être calculé dans chaque cas d'expérience. Dans le passé on employait des tables de fonctions et, pour un problème donné, on interpolait entre deux valeurs tabulées. Aujourd'hui on a recours à un programme qui calcule directement les caractéristiques des anneaux. De tels programmes utilisent des fonction de bibliothèque pour calculer les fonctions connues telle celle que nous venons d'évoquer. Une fonction de bibliothèque est un sous-ensemble de programme que le physicien emploie sans avoir à se préoccuper exactement de la façon dont il est réalisé.
Dans cet exemple la solution du problème étudié n'est donc analytique qu'en apparence. Cependant on se trouve dans une situation intermédiaire, par rapport à l'exemple précédent: la fonction numérique possède des propriétés connues qui permettent d'appréhender le phénomène physique par l'analyse de sa forme pseudo-analytique.
La physique procède d'une démarche dialectique entre théorie et expérience.
A partir d'un ensemble de faits expérimentaux le physicien étudie le comportement
d'un phénomène. Pour cela il modifie un ensemble de paramètres qui lui sont
accessibles. S'il travaille astucieusement il peut en déduire des comportements
et cela lui permet de construire une loi expérimentale. Le travail du théoricien
commence avec l'analyse de ces résultats. Grâce aux lois qu'il établit il peut
construire une théorie qui non seulement explique le phénomène étudié mais permet
de prédire le résultat de nouvelles expériences effectuées dans d'autres conditions
expérimentales. Ce schéma est évidemment idéal: il arrive que la théorie précède
l'expérience. Elle peut être construite de façon purement spéculative indépendamment
de tout contexte expérimental qui lui soit directement lié. Un des exemples
les plus éclatants de cette démarche est la théorie de la relativité restreinte
découverte par Einstein en 1905. Les faits expérimentaux dont il disposait étaient:
Son génie a été de supposer que la théorie de Maxwell restait valable dans deux repères en translation uniforme et de prendre acte de l'invariance de la vitesse de la lumière. Il ne lui restait plus qu'à appliquer les équations de Lorentz pour prédire la variabilité du temps et des longueurs. Sa théorie n'a été validée que par des observations ultérieures.
Ce mot est devenu à la mode vers la fin des années 70. Ce n'est pas un hasard: cela correspond à l'apparition d'ordinateurs suffisamment rapides pour effectuer des calculs complexes.
La simulation consiste à calculer, aussi précisément que possible, tout ou partie d'un phénomène physique au moyen d'un ordinateur. Les paramètres de l'expérience sont introduits sous forme d'un ensemble de nombres. Un programme plus ou moins compliqué calcule alors un nouvel ensemble de nombres qui représente les paramètres finaux de l'expérience que l'on veut simuler. Si on dispose d'un interface graphique suffisamment sophistiqué on peut représenter ces résultats soit sous la forme d'une image virtuelle de l'expérience soit sous la forme d'une pseudo-image ou de courbes qui permettent d'appréhender le phénomène dans sa globalité.
En microscopie électronique, par exemple, lorsqu'on étudie un échantillon de matière solide, on introduira dans l'ordinateur:
| des valeurs qui représentent la position des atomes et leurs caractéristiques du point de vue de l'interaction atome-électron. | |
| les caractéristiques du faisceau d'électrons qui traverse l'échantillon | |
| les propriétés optiques des lentilles du microscope |
Le résultat est une série de nombres qui, affichés au moyen d'un programme adapté sur l'écran d'un ordinateur, représente l'image obtenue dans une expérience virtuelle.
On voit donc qu'on ne peut simuler une expérience de physique que si on dispose d'une théorie. Dans le cas présent il s'agit de la théorie dynamique des électrons qui explique l'interaction onde électronique-matière. Il est nécessaire de traduire sous forme numérique les équations qui expriment la théorie envisagée. La précision d'une simulation dépend donc:
| des limites de validité de la théorie physique employée | |
| de la précision de sa traduction numérique |
Ce sont là les pièges les plus courants des techniques de simulation. Si on emploie un programme avec un jeu de paramètres qui correspond à des conditions en dehors de la théorie le résultat n'a évidemment aucun sens. De même si on étudie un phénomène de faible amplitude qui dépasse les limites de précision des méthodes numériques programmées dans l'ordinateur les conclusions sont erronées. Ceci se produit plus souvent qu'on ne le pense car les programmes sont souvent écrits par des personnes différentes de ceux qui les utilisent et ces derniers ne se préoccupent pas souvent des concepts sous-jacents.
La simulation permet d'effectuer des expériences impossibles ou dangereuses puisqu'on peut accéder à beaucoup plus de paramètres que dans la réalité. Mais expliquer un phénomène physique au moyen de simulations est évidemment beaucoup moins agréable pour un esprit cartésien qui rêve de pouvoir appréhender un phénomène de façon analytique. De plus l'usage de calculs numériques et de simulations n'est devenu réellement possible qu'avec l'apparition des ordinateurs capables de manipuler des nombres avec une rapidité impossible à l'esprit humain. C'est pourquoi la physique jusqu'à ces dernières cinquante ans a été essentiellement faite de simplifications qui avaient pour but de pouvoir résoudre analytiquement les équations. Bien sur cela n'était pas toujours possible: les physiciens ont eu alors recours à des tables numériques et des abaques dans les cas les plus extrêmes. Il y a trente ans encore tous les étudiants possédaient des tables numériques complexes dont l'emploi rebutant était limité aux occasions extrêmes. Mais pour l'essentiel la physique, et plus encore l'enseignement de la physique, était réduit aux phénomènes simplifiés susceptibles d'être résolus analytiquement. Cet aspect réducteur est encore celui qui est enseigné, car plus simple, dans les premières années d'études. Seuls les ingénieurs échappaient à cette tendance car ils devaient fournir des résultats précis. On a ainsi inventé des machines complexes pour calculer les amplitudes de marées car les approximations habituelles aux physiciens auraient été intolérables pour la sécurité des bateaux. Cela explique aussi que l'ordinateur est longtemps était considéré par les chercheurs comme un outil pour technicien, pas pour la compréhension des phénomènes fondamentaux.
En résumé, la simulation établit des passerelles entre théorie et expérience:
| une théorie peut être testée sans avoir besoin de faire les approximations de la physique classique | |
| on peut tester un modèle ou une théorie en comparant les résultats du calcul à ceux de l'expérience. | |
| la simulation permet d'interpréter les expériences | |
| on peut accéder à des informations impossibles à obtenir dans une expérience, par exemple en faisant varier des paramètres inaccessibles dans la réalité | |
| on peut simuler des expériences impossibles ou dangereuses |
La physique numérique permet donc d'appréhender des aspects nouveaux des phénomènes connus: les physiciens ont maintenant rarement recours à des souffleries pour étudier les phénomènes de turbulence dans les liquides et les gaz. Elle permet également d'établir des théories nouvelles comme dans le cas du chaos par exemple.
La physique numérique a recours à des méthodes numériques pour résoudre les équations mathématiques de la physique qui expriment une théorie susceptible de prédire une expérience. Le but de ce cours est d'évoquer les méthodes les plus classiques employées par les physiciens. On évoquera donc les techniques qui correspondent à l'analyse mathématique classique: intégration, différentiation, algèbre linéaire...
Cela nous amènera à discuter les approximations inhérentes à toute méthode numérique. Nous devrons nous pencher également sur leur complexité. Une méthode devant se traduire par un algorithme pour la réaliser elle peut être plus ou moins compliquée à mettre en oeuvre.
Le support, pour effectuer le calcul, est un ordinateur. Celui-ci introduit à son tour, comme nous le verrons, des limitations:
| La précision avec laquelle les nombres sont représentés dans sa mémoire est limitée | |
| Un algorithme se traduit par un ensemble d'instructions ou programme qui doivent être codées de manière adaptée. | |
| La rapidité, la capacité de stockage d'un ordinateur sont limités. Un algorithme peut être irréalisable sur une machine donnée. Si la machine suffisamment puissante n'existe pas ou n'est pas accessible cela peut obliger à faire des simplifications qu'il faudra justifier. |
Tous ces aspects seront évoqués dans ce cours.
Comme pour programmer il faut un langage nous utiliserons Fortran, et plus exactement, les parties de ce langage communes à Fortran 77 et Fortran 90. C'est en effet le langage le plus employé par les physiciens et les chimistes. Quoique le plus ancien il reste le plus adapté. Sa formulation a été concue pour résoudre des expressions mathématiques, il permet de manipuler des nombres complexes et l'écriture de programme est relativement simple. D'autres langages sont aujourd'hui plus populaires mais soit ils ne sont pas entièrement adaptés au calcul scientifique(le langage C, par exemple, ne permet pas de calculer avec des nombres complexes) soit leur complexité dépasserait le temps réservé à l'apprentissage du langage de programmation: c'est le cas de C++ par exemple. Nous excluons les langages, comme Pascal, qui ne sont employés que dans le monde universitaire et pas du tout dans l'industrie. Nous ne pouvons pas non plus utiliser des langages formels comme Mathematica ou Maple. Ils masqueraient des aspects importants d'algorithmique ainsi que les problèmes de précision numérique.
Qui parle d'ordinateur doit également évoquer son système d'exploitation, c'est à dire sa manière de fonctionner appréhendable par l'utilisateur à travers son langage de commande et l'interface graphique disponible. Il est clair qu'aujourd'hui les micro-ordinateurs sont les machines les plus populaires: Windows 95 ou MacOs sont donc des systèmes d'exploitation de choix. Cependant les ordinateurs employés pour le calcul scientifique sont le plus souvent sous système Unix. Ils disposent de meilleurs compilateurs pour le Fortran, de nombreuses bibliothèques mathématiques. Cela fait que les microordinateurs sont rarement employés pour le calcul scientifique et les compilateurs Fortran sont très onéreux. Les travaux pratiques se feront donc sur des machines Unix qui sera le système d'exploitation de référence pour ce cours.
| P. Depondt "Histoire de l'informatique " (document joint) | |
| R. Moreau "Ainsi naquit l'Informatique", Dunod 1987 |
![]()

Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 17/05/00