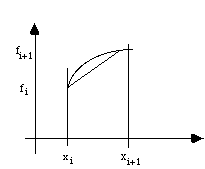
Figure 1: Principe de l'interpolation linéaire
Les expérimentateurs interpolent très souvent des fonctions échantillonnées lorsqu'il cherche à établir une loi physique à partir de séries de mesures expérimentales. On trace ou on établit l'équation de la fonction continue qui passe au mieux par les points expérimentaux. Cela est également nécessaire lorsque la fonction a été calculée au moyen d'un ordinateur: elle est forcément échantillonnée.
On emploie les techniques d'interpolation chaque fois que l'on veut connaître la valeur de la fonction en dehors des points mesurés ou calculés.
On utilise également ces techniques méthodes pour lisser une courbe: on détermine alors les coefficients d'un polynôme de degré choisi qui passe au mieux par l'ensemble des points connus. Le physicien éprouve le besoin d'effectuer de telles manipulations parce qu'il sait que le phénomène étudié est continu donc que la courbe qui le représente doit être lisse. Néanmoins il ne s'appuie, le plus souvent, sur aucune justification pour choisir le degré du polynôme employé dans le lissage. Il n'emploie aucune information nouvelle pour transformer ses mesures initiales. Bien que plus agréable à regarder la courbe obtenue n'est pas plus exacte que la série de données initiale. Il faut donc se méfier de ces manipulations qui rendent un graphe plus joli mais n'apportent en fait aucune information scientifique supplémentaire. Les américains emploient un terme cruel pour décrire ce type d'opération: "make beautify". On trouvera une discussion plus complète de ce sujet au chapitre "Méthodes de moindres carrés".
Le problème de l'interpolation se résume à la recherche de la valeur approchée d'une fonction continue f(x) en tout point x lorsqu'on la connaît seulement sous la forme d'une distribution {fi}.
C'est la technique la plus employée. Elle est souvent suffisante.
Elle consiste à remplacer l'arc de courbe inconnu par sa corde, entre deux points
d'échantillonnage.
Figure 1: Principe de l'interpolation linéaire
Ceci revient à utiliser le polynôme du premier degré:
(3.3)
pour estimer les valeurs intermédiaires entre xi et xi+1. Cette approximation est d'autant plus précis que la courbure de f(x) est grande.
Supposons que f(x) possède une dérivée seconde; on peut estimer l'erreur comme:
pour xi<=xi+1
(3.4)
Ce qu'on résume, sur l'ensemble de l'intervalle où l'on cherche à interpoler {fi} par:
où h est le pas d'échantillonnage, supposé constant et où les indices 
signifient qu'on
retient les valeurs absolues maximales des quantités qu'ils référencent.
On veut tabuler la fonction sin(x) en n+1 points entre 0 et 
et l'on désire obtenir une précision de 10-m.
Le pas d'échantillonnage est 
,
f"(x) = -sin(x), donc d'après 3.5 on
peut estimer l'erreur comme:
soit 
La valeur maximum de sin(x) est 1. On en déduit le nombre de points n nécessaire
dans l'échantillonnage: 
.
Si l'on recherche une précision de 10-6 il est nécessaire d'échantillonner la fonction sin(x) en 550 points environ pour pouvoir employer une interpolation linéaire entre deux points successifs. Si on se contente d'une précision de 10-3 18 points suffisent.
Cet exemple montre qu'augmenter la précision peut coûter très cher lorsqu'on se contente d'une interpolation linéaire. Il serait astucieux de faire varier le pas d'échantillonnage, dans les diverses zones de définition de la fonction f(x), de façon à suivre au mieux le rayon de courbure local de f(x). Là où il est grand la densité de points peut être faible. Il faut l'augmenter là où le rayon de courbure diminue. On peut imaginer un algorithme qui réalise ceci en estimant la dérivée seconde de la fonction à échantillonner en chaque point. Néanmoins ceci peut être complexe à réaliser et le calcul d'une dérivée seconde n'est pas souvent aisé. Cette amélioration des techniques d'interpolation linéaire est donc assez complexe à mettre en oeuvre et il vaut mieux recourir à des méthodes plus précises en employant des polynômes de degré plus élevé.
Le principe reste le même. Simplement on va rechercher le polynôme du second degré qui passe par trois points successifs de l'échantillonnage.
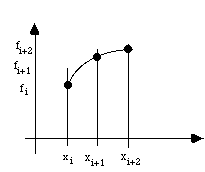
Figure 2: principe de l'interpolation parabolique
L'expression du polynôme du second degré passant par les trois points fi, fi+1, fi+2 est:
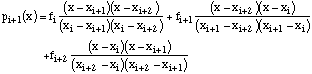(3.6)
Cette expression est simple lorsque le pas d'échantillonnage est constant. Soit h ce pas, on peut poser:
Si u = -1 x = xi, si u = 0 x = xi+1, si u = 1 x = xi+2.
En portant ces valeurs dans (3.6) il vient:
L'incertitude est majorée par le terme d'ordre 3 du développement en série de Taylor de f(x) au point xi+1:
(3.8)
Reprenons l'exemple de la fonction sin(x) déjà étudié dans le cas de l'interpolation linéaire. L'erreur est:
soit ici:
Le nombre de points échantillonnés n est donc:
soit approximativement n >= 0.6 10m/3.
La précision de 10-6 est obtenue avec 60 points seulement au lieu
de 550 précédemment, la précision de 10-3 avec 6 points au lieu de
18.
Dans le cas de la fonction sin(x) une méthode d'interpolation basée sur un polynôme du deuxième degré est déjà très efficace.
Les polynômes de Lagrange permettent de généraliser la méthode précédente au
cas d'un polynôme de degré quelconque.
On recherche le polynôme d'ordre n passant par les points {f0, f1,
..., fn}:
(3.8)
Si l'on suppose que la dérivée de f(x) d'ordre n+1 existe et qu'elle est continue,
on peut estimer l'incertitude par un majorant du terme d'ordre n+1 du développement
de cette fonction en série de Taylor:
(3.9)
ou plus simplement par:
(3.10)
Pour comprendre l'efficacité de cette technique, reprenons toujours
le même exemple de la fonction sin(x).
Supposons qu'on désire l'interpoler sur quatre points:
|
x |
0 |
|
|
|
|
sin(x) |
0 |
1/2 |
|
1 |
Nous allons employer un polynôme de Lagrange de degré 3.
En utilisant l'expression (3.8) il vient:
p3(x) = 1.0204 x - 0.0655 x2 - 0.1139 x3
L'incertitude est inférieure à 
,
ce qui signifie qu'avec quatre points on a déjà une précision de l'ordre de
10-3!
Dans le cas général la recherche des coefficients du polynôme de Lagrange est
fastidieuse.
Soient {ai} la collection des n+1 coefficients. Ils sont solutions
d'un système de n+1 équations linéaires:
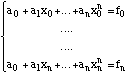
Nous étudierons au chapitre IV comment résoudre numériquement de tels systèmes. Il existe des méthodes efficaces même pour un nombre d'équations simultanées élevé.
Il est délicat de définir le degré du polynôme qu'il faut employer dans l'interpolation
d'une fonction f(x). Un polynôme de degré élevé n'est pas forcément le meilleur
choix car il peut conduire à des résultats instables. Seule l'analyse des dérivées
successives de la fonction, lorsque cela est possible, peut permettre de prévoir
ce comportement.
Reprenons, une fois encore, l'exemple d'une fonction sinusoïdale, sin(10x):
Sup|f(n)(x)| ~ 10n donc l'erreur grandit rapidement avec
n. Il serait dangereux d'augmenter trop le degré du polynôme. La figure
3 schématise ce comportement.
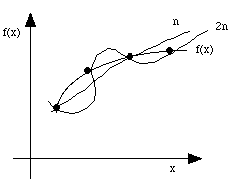
Figure 3: Approximation de la courbe f(x)
avec des polynômes de degré n et 2n respectivement.
Un polynôme de degré n peut représenter assez fidèlement la vraie courbe f(x)
alors que le polynôme de degré 2n peut osciller dangereusement autour des vraies
valeurs.
De façon générale on peut dire que:
Les oscillations d'une fonction polynomiale peuvent n'avoir aucun rapport avec la réalité de la vraie fonction. La pratique montre que jusqu'au degré 3 le résultat est en général assez bon. Au-delà il faut être très prudent. Il est rare qu'un polynôme de degré supérieur à 4 ou 5 conduise à un bon résultat. Il existe alors d'autres techniques qui peuvent permettre une meilleure interpolation.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 12/14/2001
